1.経験的な対応関係から
野球の試合に勝つということは要するに、相手の得点よりも多く得点することです。これは、ルールがそうなっているのだから議論の余地がありません。そうしてセイバーメトリクスはいかに多く得点を上げるか(Batting Runs)、いかに相手の得点を少なくするか(Pitching/Fielding Runs)といったことを徹底的に数値化し、最後にはそれを勝利数に換算するということを行っています。
得点を勝利に変換するといえば「野球版ピタゴラスの定理」と呼ばれるBill James考案のピタゴラス勝率式が定番です。しかしその式は経験的に極めてよく機能するものの「理論的に見えない」点にずっと疑問を持たれており(実際得点と勝率の対応付けを語るとき、なんでもかんでもピタゴラス勝率が使えるわけではありません)、またチームにとって適切な勝率を導く上で得点・失点だけをファクターとしていいのか、といった疑問も呈されています。
そこで、ここではまた別の観点から勝率への挑戦を見てみたいと思います。ひとつの結論に向かってというよりは繋がりをもった複数トピックのまとまりというつもりで書いていますのでその点ご了承願います。
2.確率分布で勝率予測
世の中の事象というのは、観察していくと確率的にさまざまな結果が現れる、ということがあります。例えば1日に受け取るメールの数などは、「だいたいこのぐらいの数受信する」という水準はあっても、いつも一緒とは限りません。平均が5通だとして、日によっては4通だったり6通だったりしますし、場合によっては0通ということもあるでしょう。
こういう、基本的に稀にしか起きず互いに関係のない事象が一定期間の間に何回起こったかを記録していくと、ポアソン分布と呼ばれる分布が現れることが知られています。メールの例で言えば、1日にちょうど5通受信する確率が18%で、6通受信する確率が16%で……といった具合に、1日のメール受信数という数が確率的に分布するということです。ポアソン分布は具体的には関数の形をしており、一定期間内に事象が起こる回数の平均を与えると、ちょうどX回起こる確率を導き出してくれます。
ポアソン分布に従うと言われているまた別の例は、サッカーの試合あたりの得点数です。実際に観測されたサッカーの試合あたり得点の分布とポアソン分布による理論的な分布は極めて近い形をすることがわかっています。※1
細かく考えていくと何故サッカーの試合あたり得点の分布がポアソン分布で近似できてしまうのかは不思議といえば不思議なのですが、こういうのは「細かいことはともかくとして実際に有効なら遠慮無く実をいただく」のが世間の常識ですので、そういうことにして話を進めます。
得点の分布が理論的に計算できると何が面白いかというと、例えばこんな問いに答えられることです。
「得点の平均が1点のチームと1.5点のチームでは、後者が勝つ確率はどれだけ高いのだろう?」
実際にポアソン分布で計算してみると、それぞれのチームが一試合にちょうどX点を上げる確率は以下の表のようになります。
| 点数 | 平均1点 | 平均1.5点 |
| 0 | 37% | 22% |
| 1 | 37% | 33% |
| 2 | 18% | 25% |
| 3 | 6% | 13% |
| 4 | 2% | 5% |
| 5 | 0% | 1% |
サッカーも野球と同様、試合に勝つということは相手より多くの得点を上げるということですから、この表を使えば自チームがX点で相手がX-1点以下になる場合の確率を全ての点数Xについて合計していけば、勝利の確率が計算できることがわかります。
計算してみると、平均1.5点のチームが勝つ確率が48.8%、平均1点のチームが勝つ確率が25.2%、どちらでもない(引き分け)の確率が26.0%となりました。平均1.5点のチームは約2倍も勝つ確率が高いということです(それでも実際に勝利という結末を見る可能性は5割に満たないのは意外と低く感じられるかもしれません)。
さて、対象の分布がポアソン分布に従っているということはある程度数理的に断言できることであり、以上のような計算は「比をとって2乗する」とかいうよくわからないピタゴラス勝率式による予測と比べると「理論的っぽい」感じがします。
サッカーとポアソン分布の関係に影響を受けたのかどうかは定かではありませんが、野球についても得点の分布を理論的に計算しようとした研究があります。残念ながら野球の得点の分布はポアソン分布と並べても上手くあてはまらないのですが、それでも平均得点に対応する分布を作って「ちゃんと確率を計算する」のが勝率の算出にあたっては理論的に思えるため、例えばBaseball ProspectusのClay DavenportとKeith Woolnerはポアソン分布を改造することで上手く現実に当てはまることを狙った計算式を作りました※2し、Tangotigerは自らの名前を冠した「タンゴ分布」を発表しています。※3
これらは現実の得点分布を近似するのに一定の成果を収めており、実際に勝率の推定も可能にしています。ただし、そういった研究をしても実はピタゴラス勝率にはそれほど大きな改良の余地はない(最初からかなり完成されている)ことがわかったりしました。
BPによりなされた重要な指摘は、ピタゴラス勝率は得失点の比が同じであれば常に同じ勝率を出すが実際には絶対的な得点の多さも要素として影響を持っている、というものですが、そのようなことを考慮して改良した式を作ったからといって、チームの勝率の予測という観点では大きな精度の向上は得られなかったのです。
3.Whisnant教授の論文
あるとき、米国の大学で物理学などを専門とするWhisnantという教授がこれまでになかった角度からピタゴラス勝率の改良をしてみせた論文を発表して話題を呼びました。Whisnantが提示した式は、勝率を得点と失点だけから予測することはせず、新たな要素として長打率・被長打率を組み入れています。※4
何故勝率の予測に長打率が入ってくるのか、その概要はこうです。
「ピタゴラス勝率は上手く勝率を予測することができるが、分布の形というものもまた要素になりうる。平均得点が同じふたつのチームがあっても、得点の分布の広がりが狭いほうが多く勝ちやすい。そして、長打率は分布の広がりと負の相関関係がある。単純な得失点による勝率予測と比べて、長打率が平均より.080高いチームは約1勝の積み増しを得る」
長打率が高い、すなわち本塁打などの長打に攻撃力の内容が偏っていると試合ごとに安定して得点を上げられるということはちょっと意外で、セイバーメトリシャンの間で少し物議を醸しましたが結局はやはり正しいことが確認されています。
単打や四球などの出塁に頼るチームでは、出塁があっても3アウトまでに集中しなければ得点にならず、一方で繋がるときは一気に繋がるため得点の分散が大きくなり、逆に長打に頼るチームでは出塁が一気に集中することはないかわりに出塁は確実に点になるため得点の分散が小さくなるというわけです。
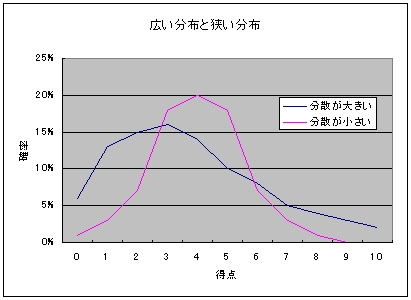
あまり見栄えの良いグラフではないですが、分布の広い狭い、分散の大きい小さいとはイメージ的にはこういう感じのものです。平均得点においては分散が大きい打線のほうが高いのですが、分散が小さい打線のほうは大量得点が少ない代わりに相手より多くの得点を上げる“頻度”は高そうだ、ということがなんとなくわかるでしょう(ちなみに、分散が小さいほうの分布は現実には有り得ないようなものを人工的に作りました)。
ピタゴラスの式のそもそもの目的が得失点と勝率を関係付けることそれだけだったとすれば、それに長打率まで持ち込んだのは別の議論です。しかし、チームの内容を勝率という形で評価することを考えるのであれば、チームに潜在している勝率への影響を考慮しない理由はなく、明らかにWhisnantの改良版が優れたモデルとなります。チームの力を語るときに、得点を稼ぐ能力・失点を防ぐ能力という一元的な量で説明するだけでは不十分であるということが示された画期的な改良でした。
ただし、その影響の大きさ自体は非常に小さく、また偶然などのノイズに埋もれやすいことはWhisnantも認めています。従ってこの効果はやたらに意識すべきものではありません。Whisnantの論文によれば、同じ平均得点でも長打率が.080高いチームは162試合で約1勝の追加的な勝利を得る、というのが定量的な結論です。得点への価値という意味では長打率は出塁率の約1/2程度だと言われていますから、通常より.080だけ長打率を上昇させて得点の利得を同じ水準に保つには出塁率を.080の半分の.040だけ減らすということになります。すなわち、長打率.400出塁率.330という一般的な水準を長打率.480出塁率.290に変えるわけです。スタッツに馴染みのある方にはすぐにわかると思いますがこれは通常ありえないほどの偏りであり、それでもやっとチームレベルで1勝、打線の9人で均等に分配すれば一人あたり0.11勝(または1.1点)の利得を得るという規模。これは、簡単に統計のノイズに埋もれる程度の数字であり、発見の興味深さからすると残念ですが評価への応用という意味での実用的な価値はあまりなさそうです。
なお、このような長打の性質のことを「同じ平均得点でも長打率の高いほうが勝利への効率が良い、実は長打は今まで思った以外の点で優れものである」と表現することができますが、この「効率が良い」という言い方は曲者です。「同じ能力なのに長打型のほうが勝てる」といった解釈まで進めてしまうと妙な誤解の元で、そもそも勝利確率を上げるためには相手より多くの得点を上げる頻度が重要なのであって、よくよく見てみれば打線の能力(質)を表すのに得点の平均値を持ち出すことがそもそも間違っていたというだけの話です。「同じ平均得点で」というのは解析者が勝手に持ち出した基準であり、その基準で揃えた比較自体に特に意味があるわけではありません。
得点の期待値に依拠していたこれまでのセイバーメトリクス観からすれば意外なのは間違いないでしょうが、これを一口に「長打は効率が良い」という表現をするのは私としてはしっくりきません。単に長打がこれまで過小評価されていただけのことです。
4.史上最強打線の意味
2004年、読売ジャイアンツの打線には他球団なら4番を打てるだろうというような打者たちがズラっと並び、終身名誉監督の長嶋茂雄氏によって「史上最強打線」といういかつい名前が与えられました。実際に259本もホームランを打ったすごい打線だったのですが、その資金力にモノをいわせた偏った補強と、結果的にチームが3位と冴えない結果だったせいか、その後の評判はあまりよろしくありません。むしろ、間違った政策の例として批判にさらされているように見えます。
あのような打線を組んだことは、やはり間違いだったのでしょうか。資金力云々はとりあえず置いておいて、ここでは科学的な側面から見てみたいと思います。
東京ドームは、傾向としては他の球場に比べて本塁打の出やすい球場です。※5 そういう環境で長距離打者を集中的に配置していくというのは、得点の要因のうち本塁打が影響する割合を大きく引き上げる、ということを意味します。つまり、どれだけ集中的に出塁するか、いかに盗塁するか、いつ犠打をするか、といったことが通常は問題になるわけですが、巨人の野球は「どれだけホームランを打つ能力があるか」ただそれだけを問題にする方向へ引き寄せられた、と言えるでしょう。
さて、ここで再びポアソン分布登場。実を言うと、得点はダメでしたが試合あたりの本塁打はポアソン分布でよく近似できるらしいことが言えます。
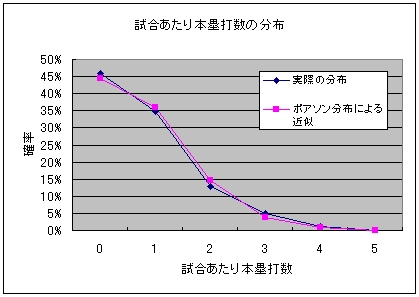
グラフは手元にあった2008年の1000試合程度(各チームランダムに混じった)のサンプルでの試合あたり本塁打の分布と、ポアソン分布による理論値です。上手く重なっているように見えます。
Whisnantが証明したように、まず、長打力に頼るチームは得点力が安定します。従って、長打力によって他のチームと同等、あるいはそれ以上の平均得点が実現できるのであればそれだけで優れた打線となります。
そして、本塁打の分布がポアソン分布で近似できるという観点からすれば、前述したような得点が本塁打に強く依存するという状態は、得点の分布がポアソン分布に寄ることを意味します。ここで、単に本塁打という要素で相手と差をつけるならば、自軍の本塁打を増やすのも相手の本塁打を減らすのも同じと考えられます。しかし、仮に思考実験としてポアソン分布による本塁打の分布を得点とみなし勝率を計算してみると、面白いことに相手の本塁打を減らすことよりも自軍の本塁打を増やすことのほうが有効なのです。自軍の平均本塁打数が2、相手が1のとき分布から計算する勝率は.768となります。これを、両方とも1/2にすると勝率は.722に、両方とも2倍すると.804になります。もちろん、自軍の本塁打を増やすというのは巨人が採用した戦略でした。
そもそも長打力というのは野球において貴重な、運や他者の影響が少なく継続的に再現が期待できる能力のひとつです。また、通常長打力のある選手は年俸が高く、いくらネタがばれても資金力のない球団には真似ができません。大砲ばかり集めても足が使えないのはダメという批判もあるようですが、本質的な意味では長打も走塁も出塁に対する進塁という意味では同じであり、長打力があれば走塁能力の欠如を埋め合わせることができること、安定した得点を上げられるという事実から「打つのを待っているだけでは調子の良い投手にあたったときに攻撃が淡白になりぱったりと打てなくなるから危険」といった批判にも必ずしもあたらないことが指摘できます。防御を考えれば足の使える選手が減ることは危険でしょうがそれは別問題ですし、また自軍も相手も本塁打の連発になることを想定すれば守備の重要性は相対的には下がります。結果を見れば、巨人のやり方は「野球を実力差が出やすくカネとチカラのあるチームが確実に勝てるホームラン競争に単純化した」と見ることができるでしょう。
このことに嫌悪感を抱く人は少なくないでしょうが、このようなやり方は兵法としては理があります。兵法というのは別に、特別で巧みな技を使って相手を負かすことではありません。物量で優位な軍は、ただ単純に物量で決まる正面衝突をし、何の面白味もなく当たり前に勝つことを目指すべきです。これまで誰も見たことがないような先進的な方策や未知の可能性がある挑戦は必要ありませんし、むしろ不確定要素が生まれますからそんなことはやってはいけません。また巨人のやり方には様々な批判があるようですが、スポーツにおいて競争優位を築こうとするひとつの試みに関してみだりに思想的・道徳的な観点から警告を鳴らすのは得策ではないでしょうし、スモールボール的スタイルに野球の理想を求める考え方にしても、ビッグボール的スタイルへの許容も残しておくほうが野球の多様性が確保されて面白いと私は考えます。
ただし本稿の意図は「史上最強打線」という試みを礼賛することではありません。あれだけ批判にさらされたものが、純粋にその中身を見ると政策的には興味深い点があるということが題材として面白い。それ以上の動機はありません。
5.伝統的なセイバーメトリクスを超える旅
メジャーリーグでセイバーメトリクス的なやり方を採り入れたチームは「新思考派」などと呼ばれたようですが、セイバーメトリクスの歴史もかれこれ数十年であり、その中での伝統的な考え方のようなものはあります。それは得点の期待値だけによる事象の価値の評価だったり、得失点と勝利の一次元的な結びつけだったり。
そこに新たな視点や分析を取り入れていくと、これまで勝率を直接に分析することの重要性や長打力の魅力・面白味がいくらか軽視されていたことが見えてきます。こういったことの発見はセイバーメトリクスらしく妙に忙しい上に些細な話の集まりですが、やはりそこには何らかの野球に対する「気付き」が隠れています。
※1 『2002 FIFA ワールドカップの得点とポアソン分布』 TAKENAKA's Web Page 2002
※2 Clay Davenport, Keith Woolner, "Revisiting the Pythagorean Theorem," Baseball Prospectus, 1999
※3 "Tango Distribution," Sabermetrics wiki
※4 "Iowa State physicist writes a better formula to predict baseball success," IOWA STATE UNIVERSITY News releases, 2010
※5 『パークファクターのページ』 日本プロ野球記録統計解析試案
なお、上記サイトの道作氏は「史上最強打線」が非効率でないことの分析も行っています。 『実はそんなに効率よくありません?』
トップ > 分析・論考 > 勝利を掴む視点
